GML Newsletter: Interpolation and Extrapolation of Graph Neural Networks
A trend is a trend is a trend, But the question is, will it bend? Will it alter its course Through some unforeseen force And come to a premature end? -- Alexander Cairncross
Hello and welcome to newcomers!
In this email, I will look into a particular line of research related to the question: can we say something about the performance of GNN on the test data?
There are two possibilities: the test data is close to the training set (interpolation or in-distribution generalization) or it is far outside of the training set (extrapolation or out-distribution generalization). In the context of graphs, to explain interpolation you can imagine that test graphs have a little bit different structure from the training set but the number of nodes and vertices is approximately the same. On the other hand, in the extrapolation test graphs can vary a lot from the training distribution, for example by having much larger sizes. So the question is for a given neural network can we say something about its generalization abilities?
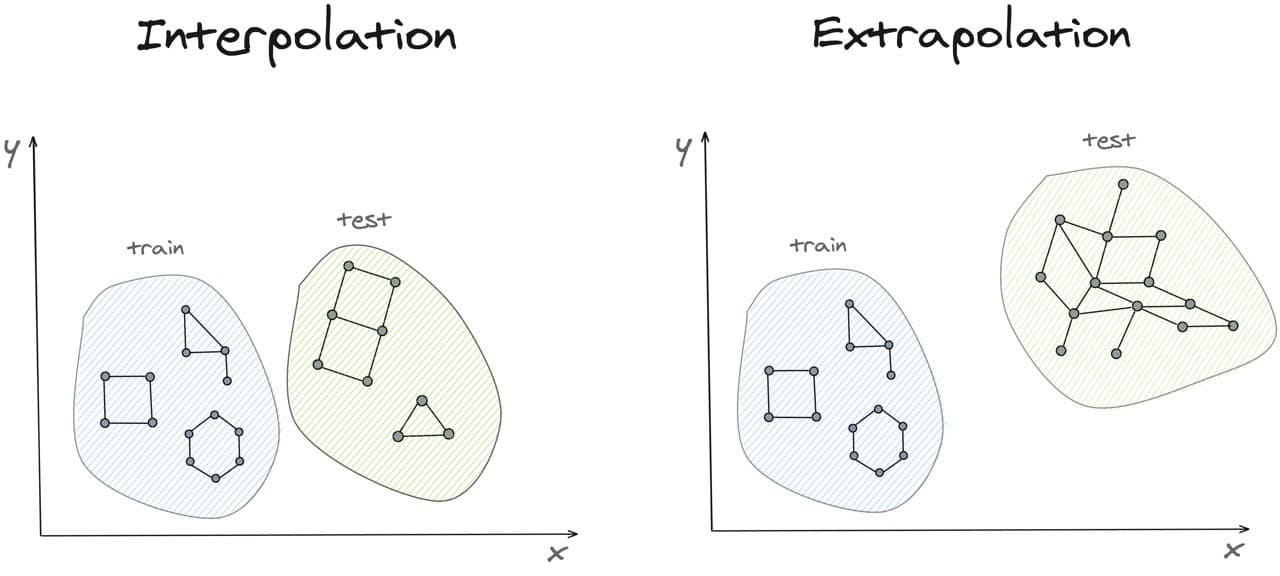
Interpolation
To analyze the generalization of ML model, we assume that there is data distribution D and that our training set S is drawn from D. We can also define two errors: empirical error and generalization error. Empirical error for model f is the error that f makes on the training set S. On the other hand, generalization error is the expectation of the model’s error on points that are generated from D. The key difference between empirical and generalizations errors is that generalization error considers expected possible test set that can be generated from D, while empirical error considers only one, i.e. S.
Interpolation can be seen as an easy case of generalization because it implies that the data in the train set and test set do not differ much (i.e. support of their data generating distributions is identical). In this case, one can bound interpolation error as a sum of empirical error and some additive term. This additive term is what researchers are constantly trying to estimate and refine for a given family of models and data distributions.
One of the recent works by Liao et al. (ICLR 2021) proposes to use PAC-Bayesian analysis to derive a generalization bound for GCNs and message-passing GNNs. Their bounds (quite scary formulas) depend on the maximum degree of the graphs, the dimension of the hidden layer, and the norm of the learned weights. The smaller these quantities are, the smaller the generalization error is. This result is a tighter bound than of Garg et al. (ICML 2020) and Scarselli et al. (2018) which use Rademacher complexity and VC dimension of the GNNs.

A couple of results exist for particular types of GNNs. Verma & Zhang (KDD 2019) studies the question of how generalization bound of a single-layer GNN depends on the randomness of SGD algorithm. The result, however, is a very loose bound as it monotonically increases as the number of SGD iterations grows. Next, Du et al. (NeurIPS 2019) derives a data-dependent generalizaton bound for graph neural tangent kernel (GNTK), a particular type of GNN. This is in turn used to show that GNTK can learn certain input functions with polynomial number of samples.
Extrapolation
Extrapolation is generalization outside of the training distribution and so it’s naturally harder than interpolation. For example, Joshi et al. (2020) show that existing GNN architectures poorly generalize in combinatorial optimization problems such as TSP and it requires additional inductive biases. However, there has been some evidence that GNNs extrapolate well on some particular tasks such as learning dynamic programming algorithms (Veličković et al. (ICLR 2020), Xu et al. (ICLR 2020)), complex particle dynamics (Sanchez-Gonzalez et al. (ICML 2020)), and branching heuristics (Kurin et al. (NeurIPS 2020)). In all cases trained GNN could retain good performance for either bigger graphs, or longer time scales, or similar but different problems.
Some works attempted to study this phenomenon in a controlled environment. For example, Knyazev et al. (NeurIPS 2019) scrutinize generalization of attention-based GNNs through ad-hoc datasets and provide recipes for more powerful architectures. Wu et al. (ICLR 2021) propose a data generation process for theorem proving that tests GNN’s generalization from 6 different angles (with different number of axioms, short or longer proofs, etc.). This work shows that GNN-based solution can have smaller out-of-distribution generalization gap than transformer-based models.
Finally, a work by Xu et al. (ICLR 2021) theoretically studies extrapolation of MLP and GNNs. First, they show that MLPs with ReLU activation function extrapolate well only if the target function is linear and training data is “diverse” enough. Other activation functions such as tanh or cos extrapolate well when target function is similar to the activation one. This suggests that incorporating non-linearity to the activation function of GNNs (aggregation and readout) can learn a function with such non-linearity. For example, if you know that target function is some form of the maximum operator, using max aggregator helps in extrapolation. While for a general task target function can be unknown, for dynamic programming algorithms, for example, min/max operators are all over the place, so it’s worth making an architecture to align with that.

That’s all for today. If you like the post, make sure to subscribe to my twitter and graph ML channel. If you want to support these newsletters there is a way to do this. Until next time!
Sergey

