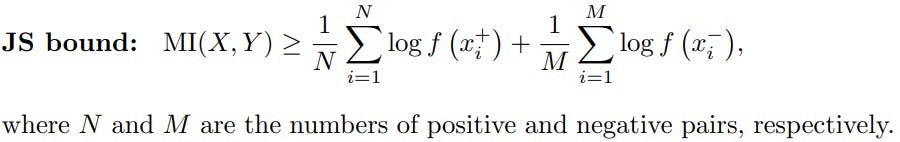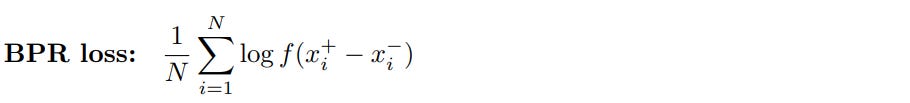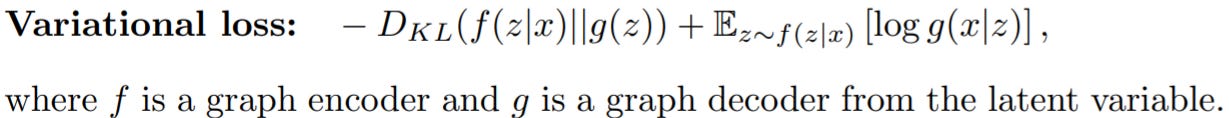GML In-Depth: three forms of self-supervised learning
"Excelling at chess has long been considered a symbol of more general intelligence. That is an incorrect assumption in my view, as pleasant as it might be." Garry Kasparov
Hello and welcome to the graph ML newsletter!
This in-depth post is about self-supervised learning (SSL) and its applications to graphs. Disclaimer: this post is long and can be clipped in gmail, in which case you can go to the web version now.
There are hundreds of works, with many surveys (e.g. one, two, three, four) and blog posts written (e.g. this and that), so it was quite overwhelming to digest, but eventually I categorized these works into three distinct groups, based on the training procedure each group has. But before going into details, let’s first define what it is.
What is self-supervised learning and how is it different from unsupervised learning?
Before ~2016, unsupervised learning (UL) and SSL were used interchangeably. Circa 2016 Yann LeCun and other researchers started using the term SSL to highlight that we have large volumes of data which we feed to neural networks to learn representations.

So now we use the term SSL when we want to say that we learn representations in unsupervised manner, while UL solves the task directly, without learning useful representations. For example, in the context of graphs there is a rich line of works on graph kernels, where graphs are represented as a histogram of some statistics (e.g. degree values) and these histograms are not learned but rather computed via an algorithm in an unsupervised manner.
Then, why self-supervised learning is such an active area of research now?
One obvious reason is that labeling the data is expensive and if we can achieve the same performance with SSL as with supervised learning by leveraging big corpuses of data it would enable all sorts of applications. But maybe more importantly, SSL would allow us to reduce the role of humans in the design choices of ML pipeline, as was outlined by Alexei Efros in his ICLR’21 keynote talk.

Specifically, SSL would allow us (a) to let the neural network cluster the objects based on the similarity of the contexts they appear instead of the human-designed label (think of the word “chair”, which is rather defined by the action “sit” and not by how it visually appears); (b) to learn on the data similarly how humans learn by always seeing a new image and (c) to omit the explicit single reward that humans design for neural networks to optimize and instead let neural networks to decide what they want to optimize next, based on the data they deal with at the moment.
Now that we understand what SSL and why do we want it, let’s look at the three forms of self-supervised learning. 🔽
SSL as property prediction
This is probably the easiest and the most explanatory type of self-supervised learning because we know exactly what our representation model predicts. Such models define a target label for each node based on the topological structure around it and the loss is cross-entropy for classification or MSE for regression between the defined target labels and the predictions of the model.
For example, S2GRL defines the target label as the hop-count between two nodes, GROVER predicts the number of node-edge types for molecules as well as if a particular motif exists in the graph. Hwang et al. show that one can boost the performance of any GNN by creating an additional SSL task of predicting a link between two nodes. Jin et al. compare regression-based tasks such as predicting the degree of a node or the distance to the cluster center.
As you can see the difference between these approaches lies only in the form of what statistics we want to predict. This approach is useful if you know what the downstream task would be. For instance, if the downstream labels correlate with the degrees of nodes then it makes sense to create an SSL task that predicts the degrees correctly. However, what to do if you don’t know where the learned representations would be used? In that case, you can resort to the second type of SSL. ⏬
SSL as contrastive learning
Contrastive learning hinges on the distinction between positive and negative views of the object. The view is defined as some perturbation of the object such as addition or removal of node or edges, subgraph sampling, or feature masking.

Most of the contrastive learning is based on the maximization of the mutual information between two random variables X and Y, where X is the target and Y is the context. In the context of graphs, X is the true or given graph G, while Y is a view of some graph (not necessarily of G).
Mutual information (MI) is the KL divergence between the joint distribution P(X, Y) which represents the distribution of positive pairs (target-positive context), and the product of the marginal distributions P(X)P(Y), which represents the distribution of negative pairs (target-negative context).
KL divergence, in turn, measures the expected number of extra information necessary to identify X and Y if they are modeled via marginal distributions instead of the joint one. If KL divergence is zero, it means that X and Y are independent, and knowing Y tells you nothing about X. So when you maximize mutual information, you want your model to distinguish well between positive pair and negative pair.
To measure mutual information one has to take the expectation of the joint P(X, Y) and marginal distributions P(X) and P(Y) and unless they are known in advance it’s impossible to compute mutual information exactly from the finite data. Instead, one approximates the true value of mutual information by maximizing some empirical lower bound of MI which could be easily computed on positive and negative pairs. The idea is that if the lower bound is close to the true value of MI, then maximizing lower bound will maximize MI too.
One of the earliest bounds is the Donsker-Varadhan (DV) lower bound, which could be estimated empirically as follows:
This bound provides the loss value for the encoder f, which is used to measure the similarity scores of positive and negative pairs. For example, graph model MVGRL compares this DV estimator to several other lower bounds discussed below.
Another popular bound is Jensen-Shannon (JS) estimator which is defined as follows:
For example, Deep Graph Infomax and InfoGraph use Jensen-Shannon on corrupted positive and negative views of the same graph. When f is sigmoid function, JS estimator is a logistic regression loss that tries to distinguish between positive and negative pairs. When K negative samples are used for each positive pair this loss is also known as negative sampling loss. Negative sampling loss has been popularized by word2vec model, which inspired several graph models such as DeepWalk, LINE, and node2vec.
Another popular lower bound is the noise contrastive estimation (NCE):
NCE bound is very similar to DV bound with the difference that NCE draws K samples per each positive and has logarithm inside the expectation in the negative part. A particular instance of NCE is called NT-Xent, which computes the similarity f(x) as a normalized temperature-scaled dot product of target and context representations. Grace and GraphCL are examples of graph models that utilize NCE loss on generated views of the same graph.
If K=1 NCE loss can be seen as a triplet loss, which was used in Subg-Con that contrasts sampled subgraphs for a given node.
Tighter bound to NCE was derived by Nguyen, Wainwright, and Jordan (NWJ):
Other contrastive losses include BPR loss, popular in the context of ranking optimization, that optimizes a sigmoid of a difference between a positive and a negative pair.
Recently Grill et al. proposed a contrastive loss BYOL which does not require generating negative samples, but works on two positive views. One may think that such loss would lead to the collapsed constant representation, however, as was shown later this loss vitally depends on the batch norm that acts as implicit contrastive learning with an average view. BYOL loss was used by BGRL algorithm on node classification task.
These losses are summarized below.
This number of choices is overwhelming so rightfully one can ask what loss function to choose in contrastive learning? Theoretically, there is a proof by McAllester and Stratos that any distribution-free lower bound (including those discussed above) on mutual information cannot be larger than O(logN) so if the true mutual information is high, then it’s infeasible to estimate it correctly with lower bounds. So from this perspective none of the bounds is good enough.
Moreover, Tschannen et al. showed that looser lower bounds can lead to better representations in downstream tasks and the success of these methods could be explained through the view of triplet-based metric learning. Given these results, it seems that the choice for particular objective should be based on the ease of computation and the downstream results that the learned representations achieve.
SSL as generative modeling
The third type of self-supervised learning tries to generate the instances of the graphs that would resemble or coincide with the ones presented in the dataset. Autoregressive generative models attempt to generate the next element given all previously generated ones in iterative fashion.
GraphRNN is one of the first autoregressive models that adds nodes one by one with an RNN encoder that adds connections for a newly added node. MolecularRNN subsequently improved this model for molecule generation by additionally considering physical properties of realistic molecules. GPT-GNN masks node attributes and edges and iteratively builds the graph by encoding each node with two GNNs for attributes and edges, respectively.
Auto-encoding generative models aim to reconstruct the entire input in one shot by passing it through an encoder-decoder pipeline. Variational auto-encoders (VAE) are an important example of this that optimizes the following loss:
VGAE was among the first to use this idea on graphs. The encoder is a simple GCN model, while the decoder generates an adjacency matrix as a dot product between latent node representations. DVNE uses Wasserstein auto-encoder that minimizes Wasserstein distance between the data distribution and the encoded training distribution.
The goal of adversarial generative models is to train two networks, one that generates objects (generator) and one that discriminates between the true objects and the generated ones (discriminator). Note that generator does not have to produce entire graphs, but can output graph-related statistics such as connectivity, random walks, or subgraphs.
GraphGAN is one example of adversarial graph model where generator predicts connectivity of every node, which is subsequently discriminated against the true ones. Next, NetGAN has a generator that produces random walks from a latent variable which are then compared against the random walks from the true graph. MolGAN takes this idea further and generates entire graphs of pre-defined size at once by MLP, which are compared against true molecules.
As you can see there are plenty of methods for obtaining self-supervised representations so it’s natural to ask:
Which self-supervised model should I pick for my task?
And as you may guess there is no silver bullet for all downstream tasks but rather an entire toolbox you can use to approach your problem. However, some general strategies exist to narrow down the search.
As said above, property prediction SSL excels at tasks where the auxiliary label correlates with the target label of the downstream task. For example, in the context of recommendation one may predict the number of views of each product as a proxy for the more precise and rarely available label such as the number of purchases of a product.
Contrastive SSL is a very active area of research right now and is considered to be state-of-the-art for many tasks in computer vision. Recent breakthroughs in this area, including such models as SwAV, MoCo, and SimCLR achieved classification accuracy on ImageNet close to the supervised methods, even though they don’t use true labels.
Finally, generative SSL is able to learn the underlying distribution of the data without assumptions of the downstream tasks and as such achieves phenomenal results in natural language modeling in models such as GPT-3 and BERT. Hence, if your learned representations are going to be used in the generation of new objects (texts, audios, or graphs), then generative SSL should be a default choice.
That’s all for today 👋 If you like the post 👍, make sure to subscribe to my twitter 🐦and graph ML telegram channel 📝 You can support these emails by subscribing to this newsletter 📧 Until next time!
Sergey